ＦＥＭ基礎理論　ＦＥＭ（有限要素法）基礎理論

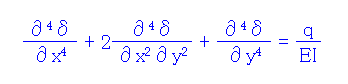
複雑な境界条件の元にてこれを解きδを求めるのは一般に不可能な場合が多い。
単純な長方形板ではなく、　複雑な形状の部材となればなおの事、編微分方程式は解が存在しなかったり、　解く事は難しい。

この欠点を克服するために考え出されたのが有限要素法、　すなはち”離散化素分割）によって複雑な形状の解析対象物を簡単な形状の要素　の集合体としてとらえ各々要素についてたてた釣り合い方程式を対象物全体の方程式に組み上げて解く。”　　というものである。

〇　離散化の前提条件
・　隣り合う要素間では節点を通じてのみ力を伝え合う。
・　隣り合う要素は節点を共有しているので節点にて変位は連続している。
・　外力や物体力は節点にしかかけられない（等価節点力の導入）
・　拘束位＝0や強制変位も節点変位に与えられる。

〇　弾性体の条件
・　変形量が少なく、荷重と変位に比例関係が成り立つ。　Ｆ＝Ｋｘ
・　材料は等方性で一様である。
・　荷重を取り除くと元の形に戻る。

この離散化手法により、無限の自由度を持つ連続体微分方程式を有限自由度（節点のみの自由度）に低減でき難解な編微分方程式は簡単な連立一次方程式に置きかえる事ができる。

２．　有限要素法の特徴
・　メッシュ（要素）を細かくするほど元の連続体に近づくので解析精度が上がる。
・　反面、連立一次方程式の行列が増えるので解析時間が爆発的に増える。
・　材料力学や、弾性力学の様に弾性体の形状による制限を受けない。
・　複雑な境界条件にも対応可能。
・　解析結果の足しこみができる。
・　異なる要素（ソリッド、シェル、ビーム）の混成モデルが可能。

３.　ソリッド要素のつりあい方程式
・　離散化された要素（メッシュ）ごとにつりあい方程式を立てる。

　　　要素釣り合い方程式は

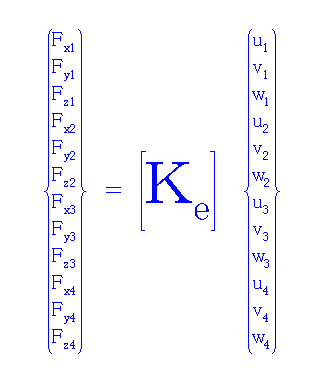
Ｆは各節点のＸ，Ｙ，Ｚ方向の力成分、　u,　v,　w　各節点のＸ，Ｙ，Ｚ方向変位成分、　［Ke］　は要素剛性マトリクスで要素形状、材質（ヤング率、ポアソン比）を含む　要素の剛性（変形かたさ）を表すマトリクス。

この要素剛性マトリクス［Ke］は、　前述した”弾性力学の基礎”のなかで紹介している　”変位と歪の関係式”　と”応力と歪の関係式”　を用い、更に要素内の変形状態を表す変位関数を導入する事によって求める。

求められた、要素釣り合い方程式を弾性体全域に渡っての足し込み処理を行う。

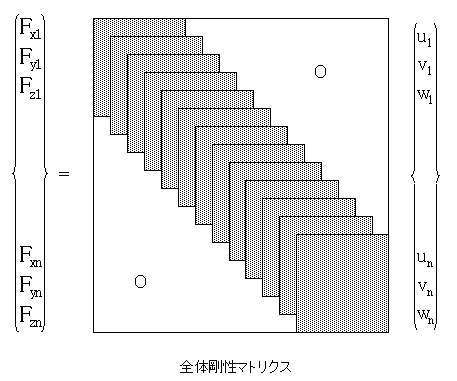
束条件定する節点に0を代入）適用し、外力適用点に実際の力と等価な力（N）を代入、その他には0を入れて　この連立方程式を解けば　未知の節点変位

u1 v1 w1 u2 v2 w2 u3 v3 w3 ・・・・・・　 uｎ vｎ wｎ　　　が求まる。　　＝＝＞　変形図作成

求められた節点変位と形状関数を使い、　要素内の任意の点の変位を求め、　弾性力学の　”変位－ひずみ方程式”　と　”応力ーひずみの方程式”　より　その点の応力を求める事ができる。　　＝＝＞　応力コンター図作成

これが有限要素法の基本プロセスとなる。