ＦＥＭ基礎理論　弾性力学の基礎（一般３次元問題：ソリッド要素）

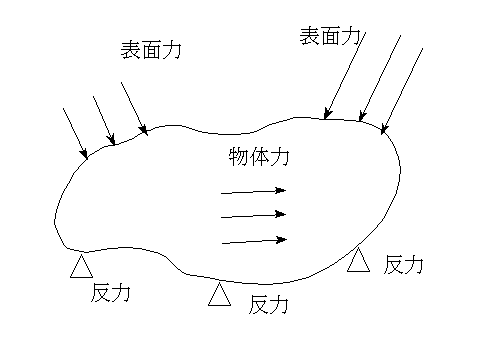
〇　弾性体に作用する力

表面力　：　物体の表面より作用する力　（すなはち外力）
物体力　：　物体の内部に直接作用する力　（重力、遠心力など）
内力　　：　外力によって弾性体が変形する時、それらに抵抗する力
反力　：　表面力や物体力が弾性体に作用する時、物体を拘束していなければ加速度運動を始めてしまう。
　　　　　これを押さえるための拘束面には反力が生じている。
　　　　　物体力＋表面力＝反力の関係が成り立っている。

２．弾性体の３次元応力状態
弾性体の内部における任意の点の微小立方体を仮想的に取り出し、Ｘ，Ｙ，Ｚ座標を用いて応力状態を定義する。

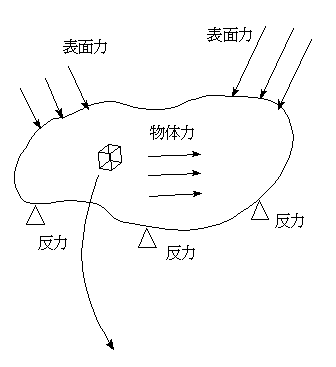
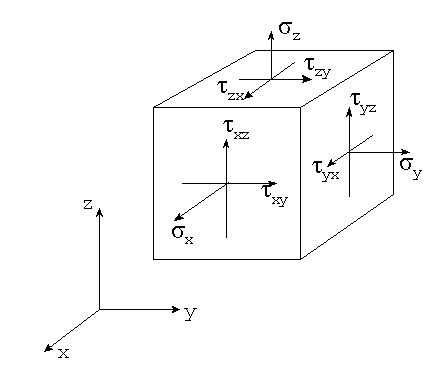
〇　応力とは
弾性体に外力が作用する時、それに抵抗する力（内力）が生じるが、単位面積あたりの内力を応力という。　-＞　物体内部の力のかかり具合をみる指標。

垂直応力　：　σｘ　σｙ　σｚ　の　３成分
せん断応力　：　τｘｙ　τｘｚ　τｙｘ　τｙｚ　τｚｘ　τｚｙ　の　６成分
（６面体の面に平行にかかる応力で面をずらす力。  τｘｙ = τｙｘ , τｙｚ = τｚｙ, τｘｚ = τｚｘ が成立つ。）

〇　歪とは
応力によって生じた変形の度合いを表すための物理量で単位長さあたりの変形量。

垂直応力σに対して　－-　垂直歪み　ε
せん断応力τに対して　-＞　せん断歪み　γ   で、以下の対応がなりたつ。

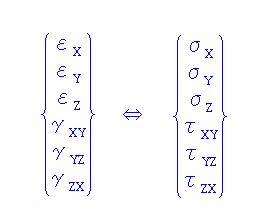
〇　ポアソン比とは
σｘ　によって垂直ひずみεｘが生ずる時、　Y、Z　方向にも　εｙεｚが生じている。　この時の歪の比率をポアソン比という。
Ⅹ方向歪、Y方向歪、Z方向歪の関係は　ポアソン比を用いて　　εｙ 　＝　εｚ　＝　－νεｘ　となる。

物体が変形した時、微小立方体の変形量（変位）を　u、ｖ、ｗ　（ｘ、ｙ、ｚ方向に対応）とすれば、変位と歪の関係式は以下となる。

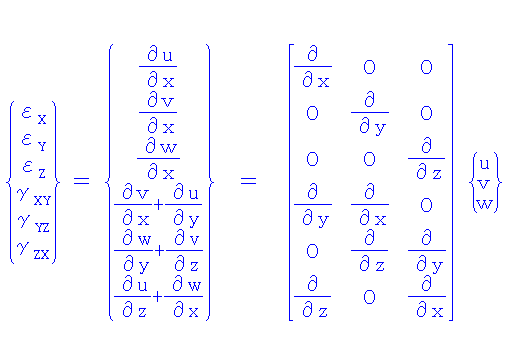
単軸応力状態の応力と歪の関係式　σ＝Ｅε　を３次元的に適用すれば以下の関係式が導かれる。

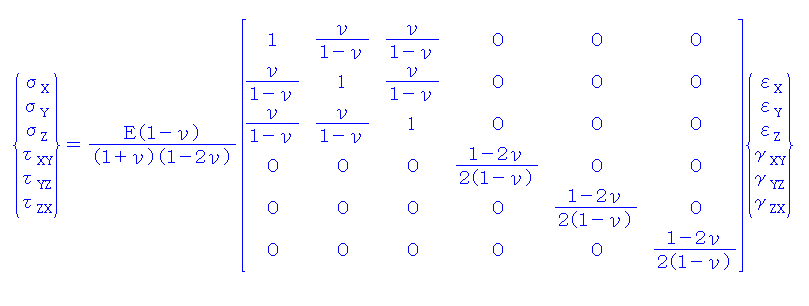
これら上式　2つが有限要素法でのソリッド要素の要素マトリクス作成の基礎となる。