ＦＥＭ基礎理論　強度評価理論

材料の単軸引っ張り試験は一般に以下の様な試験片を使用し行われる。この実験による結果と有限要素法によって得られた３軸応力状態の値を突き合わせていく。

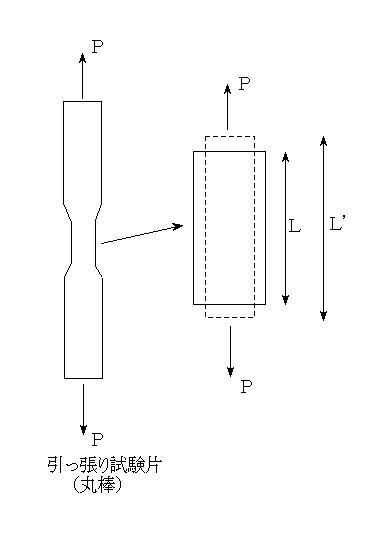
１．ます主応力を求める。
主応力とは　：　弾性体の任意の点について考えた微小立方体は仮想的に切り出したものである。
立方体の向きはｘ、ｙ、ｚ　軸周りに任意に回転させても良い。　上手に回転させると、τｘｙ　τｙｚ　τｚｘ　のせん断応力をすべて０にする角度が存在する。

このときの垂直応力　σ１　σ２　σ3　　を主応力、中間主応力、最小主応力と呼ぶ.

σ１　＞　σ２　＞　σ3　　と定める。

微小立方体の回転を表現するための方向余弦（ｘ、ｙ、ｚ軸とのなす角が成分）を導入して　τｘｙ　τｙｚ　τｚｘ　を　すべて　０にする角度を探したとき、主応力は次式を満足する解で与えられる。

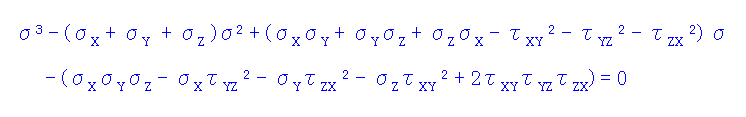
上式を解いて得られた3つの解を大きいほから、　主応力　σ１　σ２　σ３　とする。

２.　強度理論（求めた主応力を利用し、各種強度評価理論を展開する。）

強度理論にはフォン ミーゼス説、　最大せん断応力説（トレスカの説）、最大主応力説　などがある。
各理論によって相当応力σeを求め、単軸引っ張りでの実験による降伏応力とを比較検討する。　

相当応力σe : 単軸引っ張り応力と比較するために導入された応力値。
3軸の応力値より表現される。

A）ヴォン　ミーゼス説

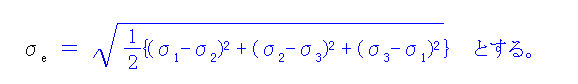
材料の単位体積当たりのせん断エネルギーが（σｘ　σｙ　σｚ　τｘｙ　τｙｚ　τｚｘ）　1軸引っ張り試験における　材料の単位体積当たりのせん断エネルギーを超える場合　破断するという仮定より導かれている。

B）最大せん断応力説（トレスカの説
　　

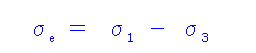
塑性変形の始まり料の降伏が始まるは材料の結晶内ですべりが始まることであり、すべりとはせん断変形である事に注目した理論。　１軸引っ張り試験でのせん断応力が3軸応力状態でのせん断応力　τ＝（σ１　－　σ3　）／2　を超えた場合に破断するという理論。

C）最大主応力説

１軸引っ張りでの応力と３軸状態での最大主応力σ１　を超えた場合に破断するとした説。

以上の評価理論を用い、構造解析での結果と単軸引っ張りでの実験結果を比較する。　更に安全率を考慮したうえで破断や破壊を起さない様、設計段階にて対策をとっていく。